Cabc-(Cab)n-Cabc型分子旋光异构体个数的计算！

一. 首先我们要先理清一个概念，什么叫做旋光异构体？

旋光异构体：是指构造相同，构型不同，从而导致旋光能力不同的同分异构体。这里说的是旋光能力不同，而不是一定要具有旋光。内消旋体虽然没有手性，旋光度为0，但与含手性旋光度不为零的异构体间的旋光能力就是不同的，所以依然算作旋光异构体的成员。

二. 我们在学习旋光异构体个数的计算时，当分子中没有对称因素存在时，一般旋光异构体的个数为2ⁿ个，n为手性中心的个数，例如下面这个化合物含3个手性中心，具有8个旋光异构体。

三. 但是当化合物具有对称因素时，就有可能产生内消旋体，旋光异构体的数量就会减少，例如酒石酸的旋光异构体：

四. 对于上面的酒石酸分子，是一类R-(C_ab)_n-R型的分子，R表示碳链两端相同的非手性基团，中间的碳都连有a、b两个原子或基团。酒石酸中两端的羧基就是相同的非手性基团（将羧基换成甲基，乙基，卤素等其它非手性的基团也可以，但不能与a或b相同，），中间的两个碳连的都是一个H和一个-OH，对于这种形式的分子，其旋光异构体有计算公式，这里要分两种情况：

1. 当n为偶数时，该分子具有2^n-1个光活异构体（有手性的）和2^（n-2）/2个内消旋体（没有手性的）。例如上面的酒石酸，n等于2，是偶数，那么就有2^2-1=2个具有手性的光活异构体（化合物C和D），和2^（2-2）/2=1个内消旋体（化合物A或B，同一化合物），总共加起来有3个旋光异构体：

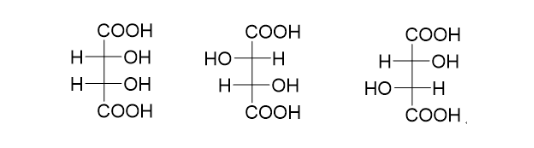
2. 当n为奇数时，该分子共有2^n-1个旋光异构体，其中有2^（n-1）/2个为内消旋体。例如下面这个化合物，n等于3，是奇数，那么总共有2^3-1=4个旋光异构体，其中包含了2^（3-1）/2=2个内消旋体。

再例如下面这个化合物，n等于4，符合偶数公式，含有2^4-1=8个具有手性的光活异构体，和2^（4-2）/2=2个内消旋体，即使不画出来，我们也能知道总共加起来有10个旋光异构体。

                                                                                                                                                                                         引自盛涛  有机化学大讲堂